Cuando analizas un metaanálisis, ¿solamente lees sus conclusiones? Nosotros antes lo hacíamos así, hasta que descubrimos (con horror) que las conclusiones de l@s autores/as no siempre describen fielmente los resultados de sus metaanálisis, e incluso que los resultados resaltados por los autores no siempre son los más relevantes.
Los metaanálisis son uno de los mayores logros de la medicina y la investigación de las últimas tres décadas. Además, son un instrumento necesario, o incluso crucial, en el proceso de transmisión del conocimiento, que se utiliza (cuando es posible) como punto de partida para desarrollar guías de práctica basadas en la evidencia (o sumarios de evidencia). Por eso, para cualquier profesional de la salud es fundamental saber cómo encontrar revisiones sistemáticas o metaanálisis de alta calidad y, por supuesto, debería disponer de los recursos suficientes para interpretarlos. Este último es justamente el tema que intentaremos abordar en esta entrada.
Pero vayamos al principio, ¿qué es un metaanálisis?
Un metaanálisis es una revisión sistemática que combina los resultados de estudios independientes y los analiza utilizando un método cuantitativo. Como herramienta de síntesis, el metaanálisis debe resumir toda la información disponible de una manera no sesgada y rigurosa, siguiendo un proceso sistemático, explícito y transparente.
Los ensayos bien diseñados y con muestras grandes son escasos y muchos de los estudios individuales existentes son demasiado pequeños para detectar efectos concretos. Asimismo, en la literatura científica podemos encontrar estudios con efectos contradictorios (efectos que apuntan en sentidos opuestas). Los metaanálisis nos permiten analizar estudios con diferentes tamaños de muestra o contradictorios, y al combinarlos obtenemos un resultado que apunta en una sóla dirección y cuyo tamaño de muestra y capacidad para evaluar los efectos de interés es mucho mayor.
· Sintetizar e integrar los resultados de varios estudios individuales.
· Analizar las diferencias en los resultados entre estudios.
· Aumentar el poder de detectar un efecto de interés.
· Mejorar la precisión en la estimación de los efectos.
· Evaluar los efectos en subgrupos de pacientes.
· Determinar si se requieren nuevos estudios (o unificar metodologías) para un tema concreto.
· Generar nuevas hipótesis para futuros estudios.
El objetivo final de los metaanálisis no es establecer una recomendación, sino ofrecer un análisis del estado actual del conocimiento, tanto de los estudios a favor como en contra.
Interpretando los resultados
Las conclusiones de un metaanálisis siempre deberían establecerse como clara respuesta a la pregunta formulada del estudio y en base a los resultados obtenidos. En ningún caso los autores deberían establecer recomendaciones para la práctica diaria en base a sus resultados (existen más aspectos que deben tenerse en cuenta para realizar dichas recomendaciones) ni extralimitarse en ninguna de sus conclusiones. El protocolo del estudio debe quedar fijado y establecido previamente (registrándolo si pudiera ser), pero a veces, cuando los resultados que arroja el metaanálisis no son estadísticamente significativos, algunos autores acaban sacando conclusiones secundarias al análisis de datos, olvidando incluso la(s) pregunta(s) que intentaba responder inicialmente. Más allá de las conclusiones que los autores puedan sacar de sus resultados, ser capaces de interpretar estos últimos de forma independiente nos dará más herramientas para entender sus posibles implicaciones reales, así como detectar conclusiones que no acaban de corresponderse con los hallazgos.
Los resultados de un metaanálisis se organizan a través de un gráfico llamado forest plot (diagrama de bosque).
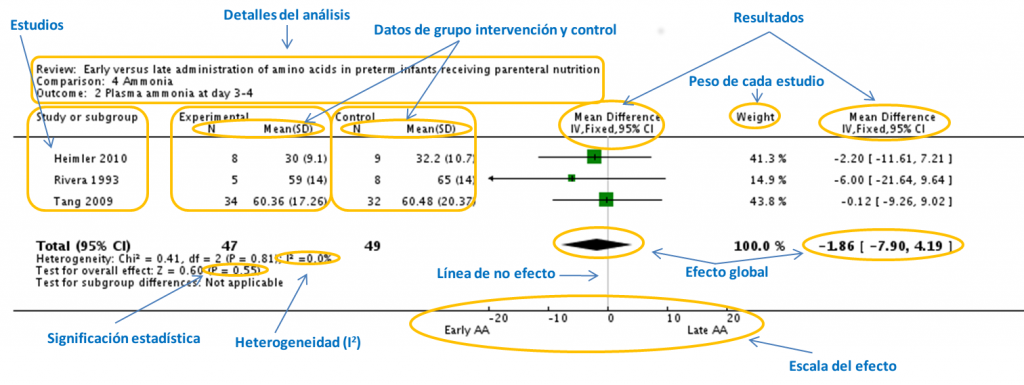
Ejemplo de un forest plot en el que se detallan sus elementos. Modificado de: Trivedi A, Sinn JKH. Early versus late administration of amino acids in preterm infants receiving parenteral nutrition. Cochrane Database Syst Rev. 2013;7:CD008771.
Generalmente, un forest plot se divide en seis columnas y los resultados individuales de cada estudio se disponen en filas sucesivas.
En la primera columna se presenta el listado con la identificación de los estudios individuales incluidos. Cuando se ha realizado un análisis de subgrupos, estos se muestran también en la primera columna. Es importante tener en cuenta que el análisis de subgrupos debería haberse indicado en el protocolo del metaanálisis, ya que algunos autores tienen la tentación de hacer subgrupos a posteriori para intentar obtener resultados estadísticamente significativos. También hay que fijarse en que los estudios que se indican en esta primera columna deben presentar una metodología y diseño semejantes, ya que no es adecuado mezclar o agregar datos de estudios que analizan diferentes especies o diseños dispares (estudios aleatorizados controlados, estudios de cohortes, estudio in vitro, etc.). En el forest-plot de este ejemplo se puede ver (con sorpresa) cómo se mezclan datos de estudios realizados en humanos y datos de estudios realizados en animales.
La segunda columna representa a los grupos intervención y la tercera a los grupos control. Estas dos columnas pueden presentar subcolumnas, que hacen referencia al tamaño de la muestra (n) y a la media de los resultados individuales y sus desviaciones estándar (mean (SD), o bien a riesgos relativos (RR)).
La cuarta columna es una representación visual de los resultados de los estudios (en algunos metaanálisis, esta información puede presentarse en la sexta columna). La línea vertical central de esta representación es la línea de ‘no efecto’, la cual simboliza que no hay diferencia entre el grupo de intervención y el grupo control. En metaanálisis con variables dicotómicas o binarias (por ejemplo, sí/no, enfermedad/no enfermedad, etc.), la línea tiene el valor de «uno» porque representa un ratio (el riesgo relativo o el odds ratio); a diferencia de estudios con variables continuas (por ejemplo, peso, colesterol, niveles de glucosa en sangre, etc.), donde la línea de no efecto tiene el valor de «cero». Ambos lados de la línea, simbolizan si los resultados favorecen o no la intervención, pero ojo, aunque es habitual ver el “favorece a la intervención” a la izquierda de la línea de no efecto, esto no es siempre así y, si no se hace una lectura más detenida, se puede malinterpretar la gráfica.
Dentro de la gráfica, los cuadrados representan el efecto evaluado en cada estudio y su tamaño está directamente relacionado con el peso de los estudios en el metaanálisis (expresado numéricamente en la quinta columna). La línea horizontal que los atraviesa representa el intervalo de confianza. Cuanto más larga sea la línea, mayor será el intervalo y, por tanto, los resultados del estudio serán menos precisos (una flecha en los extremos, indica que el intervalo es mayor que el espacio disponible). Los efectos individuales (los cuadrados), se posicionarán a izquierda, derecha o sobre la línea de no efecto, dependiendo del resultado individual obtenido en cada estudio. Si la mayoría de efectos se posiciona a un lado de la línea de referencia, esto indica que la heterogeneidad es baja, pero cuando los efectos se distribuyen a ambos lados, significa que los estudios son contradictorios (la heterogeneidad es alta) y las conclusiones del metaanálisis se pueden ver comprometidas.
Los intervalos de confianza permiten conocer la precisión de la estimación dentro de un margen de error establecido. El IC 95% (p=0,05) se considera suficiente (aunque se puede utilizar el IC 99% [p=0,01]; pero es poco habitual), representa una seguridad del 95% de que la asociación estudiada no se da por el azar.
Los diamantes representan los resultados globales del metaanálisis, ya sea del análisis de subgrupos realizados (subtotales) o bien del conjunto de todos los grupos (total). El centro del diamante es el valor del efecto en conjunto y el ancho representa el intervalo de confianza general. La diferencia entre los grupos de intervención y control puede considerarse estadísticamente significativa, si el diamante se posiciona claramente a un lado de la línea de referencia, pero si la cruza o simplemente la roza, no se podrán sacar conclusiones que apunten en una dirección.
Todas las representaciones gráficas que acabamos de comentar, tienen su traducción numérica en la quinta y sexta columna. La quinta columna representa el peso de cada estudio sobre el resultado global (cuanto mayor sea el tamaño de la muestra y más estrecho sea el intervalo de confianza, mayor será el peso del estudio). Es fácil comprender que si un solo estudio tiene mucho peso, ejercerá una gran influencia en el resultado final del metaanálisis, de modo que si este estudio tiene una calidad metodológica dudosa, podría hacer que los resultados globales fueran engañosos. Para intentar evitar este tipo de errores y determinar la solidez de los resultados del metaanálisis, los autores deberían aplicar un análisis de sensibilidad, que consiste simplemente en presentar los resultados cuando se quitan algunos estudios del análisis. Si esto provoca cambios importantes en los resultados globales, como una modificación de la dirección del efecto, los resultados del metaanálisis deben interpretarse con cautela; si por el contrario sólo se altera el tamaño del efecto, el resultado puede considerarse firme. Esto es tan importante que las conclusiones de los autores deberían ir acordes a estas consideraciones.
La sexta columna expresa los resultados numéricos de cada estudio. Concretamente, en metaanálisis con variables dicotómicas se presenta el riesgo relativo (el cociente del riesgo en el grupo intervención entre el del grupo control de cada estudio) y en metaanálisis con variables continuas se presenta la diferencia de medias (diferencia entre la media del grupo intervención y el control de cada estudio), con su intervalo de confianza correspondiente. Para que los resultados individuales sean estadísticamente significativos, en el caso de variables dicotómicas, el intervalo de confianza no debe incluir el valor 1, mientras que en variables continuas, no debe incluir el 0.
Los datos numéricos se incluyen en el abstract de cada metaanálisis, por lo que con una simple lectura del mismo, deberíamos ser capaces de evaluar si los resultados son estadísticamente significativos o no (independientemanete de lo que digan los autores).
Al final de esta presentación de datos, el forest plot incluye la prueba de heterogeneidad (I2), que mide la variabilidad entre estudios, indicando cómo de comparables son los estudios analizados. Los datos de los estudios individuales se pueden analizar en el metaanálisis utilizando el modelo de efectos fijos (fixed effect model) o el de efectos aleatorios (random effect model).
Resumidamente, el modelo de efectos fijos asume que el efecto del tratamiento es el mismo en todos los estudios, mientras que el modelo de efectos aleatorios asume que los efectos del tratamiento no son los mismos en todos los estudios. Cuando el nivel de heterogeneidad entre los estudios es elevado, el resultado del metaanálisis probablemente dependa del modelo utilizado y en estos casos, el análisis debería realizarse y presentarse usando ambos modelos.
Finalmente, el forest plot muestra un apartado que presenta el test de efecto global, que mide la significación estadística del resultado del metaanálisis. Un resultado se considera estadísticamente significativo cuando el valor de la «p» es inferior a 0,05 (para IC 95%). Cuando no hay diferencia estadísticamente significativa (el valor es superior a 0,05), los autores no deberían resaltar ninguna conclusión que apuntara en un sentido concreto, es decir, deberían abstenerse de realizar consideraciones del tipo: «aunque los resultados no son estadísticamente significativos, esta terapia muestra una tendencia a mostrar efectos positivos en favor del grupo intervención» o similares. De todos modos, hay que tener presente que el término estadísticamente significativo no es lo mismo que tener efectos relevantes, ya que una asociación estadísticamente significativa puede no ser clínica o epidemiológicamente relevante. Por eso, siempre debe entenderse en el contexto del estudio, su diseño, las características de la muestra o la población, etc. El valor de «p” no debe ser una cifra mágica que autorice a dar recomendaciones.
 En resumen, en un forest plot hay que fijarse en:
En resumen, en un forest plot hay que fijarse en:
- · La heterogeneidad de los efectos.
- · El peso de los estudios.
- · Los intervalos de confianza.
- · La disposición del diamante.
- · El test de efecto global.
Lectura recomendada: interpretando y entendiendo un forest plot
Para aumentar vuestra habilidad para interpretar un metaanálisis, es muy recomendable leer algunos manuales de elaboración (para revisiones sistemáticas y metaanálisis) que pueden obtenerse libremente on-line, como el de la Colaboración Cochrane o de la Universidad de York. También os invitamos a que echéis un vistazo a las propuestas concretas para adaptar los métodos genéricos al ámbito específico de la nutrición.
Recomendación para súper motivados: si necesitas preparar un forest plot para tu metaanálisis, Cochrane dispone de un software, compatible con cualquier sistema operativo, que puedes descargar de forma gratuita y que es relativamente fácil de utilizar: RevMan
Esperamos que encontréis esta entrada de utilidad para aumentar vuestra habilidad de interpretación de metaanálisis. En las próximas entradas, os daremos más herramientas para la evaluación crítica de un metaanálisis.